Why is Complexity So Complex?

Information and Complexity: Essay 5

The underlying structure of the universe is simple¹.

Which, frankly, makes absolutely no sense.

Because this same universe gives us apple trees, ant colonies, thunderstorms, stock markets, seven seasons of Black Mirror, democracy, Jupiter, the platform formerly known as Twitter — and physicists who say the underlying structure of the universe is simple.

This article is about complexity. Which, annoyingly — or maybe just appropriately — is a complex topic.

Newtonian and quantum physics have done a great job explaining the fundamentals.
Newton’s laws help us predict the motion of planets and projectiles. Quantum theory lets us model the strange behaviour of particles and atoms. These theories are incredibly good at predicting what happens at both large and small scales (at least in our part of the universe). The math is astonishingly precise.

But these theories haven’t yet told us much about how we get complex things like cells, weather patterns, economies, and societies, from simpler building blocks. Let alone the things we explore in this newsletter: brains, artificial intelligence, and — the mother of all complex things — consciousness.

These are the next big questions in science. Complexity science is still a young science — and right now, there are far more questions than answers. But it’s one of the most exciting frontiers in science.

In future essays, I’d like to look at what complexity science might have to say about consciousness — or at least whether it gets us anywhere interesting.

So where do we begin?

Complexity isn’t something we’re going to pin down in a single essay. Sorry. But let’s see if we can start to unpack the puzzle.

Our three guiding questions are:

1. Can We Define Complexity?

2. Where Does Complexity Come From?, and

3. Is Life a Special Kind of Complexity?

Just a quick heads-up before we start:

1. There’s no single definition of complexity — and plenty of ways people have tried to measure it. In this essay, I’m going to highlight three key features of complex systems (☝️✌️🤟) and three major attempts to quantify it (1️⃣ 2️⃣ 3️⃣). Just know: there are far more ways to define and measure complexity than I’ll be able to cover here.

2. Because complexity science is still a relatively new and evolving field, many of the ideas in this essay are active areas of research. I’ve added footnotes where I think it’s helpful to flag open questions, differing views, or places where the science is still being figured out.

3. And finally, this is essay 5 in the series on Information and Complexity. I’ll be drawing on ideas from earlier essays (especially Essay 3) — but don’t worry, you don’t need to have read the earlier essays to make sense of this one.

---

Q1: Can We Define Complexity?

Complexity is difficult to define — which is odd, really, because it seems pretty easy to recognise.

I think (almost) all of us would agree that a brain is complex. And I think most of us would say an apple tree is complex, but probably not as complex as a brain. What about a rock? Not so much. I think most of us would probably say a rock seems fairly simple.

So what is it about a brain that makes it different from a rock? At the deepest level, they’re both made of the same fundamental particles — atoms, quarks, electrons. They follow the same physical laws. And yet one of them thinks, feels, remembers, and dreams — while the other just sits there, being a rock.

☝️ Here’s the first thing to note about complex systems…

They resist reduction. You can break a brain down into atoms, quarks, and electrons — and yes, they all obey the laws of physics. But that alone doesn’t tell you how memory works. Or why a joke makes you laugh.

Even molecular or cellular models often fall short when trying to explain things like emotion or consciousness. These aren’t just properties of the parts — they emerge from the interactions between them.

Brains — like other complex systems — behave in ways that only make sense when you zoom out and consider the whole.

In other words: complex things have emergent properties.

A Quick Note About Emergence

Not everyone loves the word emergence. And fair enough — it can sound a little magical, as if something just appears out of nowhere.

But in physics, emergence isn’t spooky. Complex systems still follow the same physical laws — nothing extra is added. What makes them emergent is that the behaviour of the whole can’t easily be predicted by analysing the parts in isolation. The key lies in how those parts are arranged and how they interact.

The more complex the system, the more of these emergent behaviours we tend to see.

Scientists like to measure things. They like equations. Pointing at a brain and saying it has more emergent properties than a rock might feel satisfying — but it’s not very rigorous. Scientists want to be able to show — mathematically — that a rock is less complex than a brain².

That’s a big ask.

But it hasn’t stopped people from trying.

1️⃣ Algorithmic Complexity

(is our first measure of complexity)

And out of all the measures it’s the most formal attempt. It’s also known as Kolmogorov complexity.

Imagine you want to reproduce a pattern — let’s say you want to reproduce the string of letters that make up the text in your favourite novel — using a computer program. The algorithmic complexity of that pattern is the length of the shortest possible program that can generate your favourite novel.

The simpler the pattern, the shorter the program. The more complex the pattern, the longer the program has to be.

Take a repeating string like ABABABAB... That pattern is easy to generate. It’s simply a short program that says repeat AB x times. But a novel requires far more instructions — there’s no simple shortcut.

Algorithmic complexity is an elegant way to measure complexity. And it works well for things that have structure — like patterned data streams or digital photographs. But it runs into trouble when there’s no structure — like with a random string of letters.

The shortest possible program to generate a truly random string of letters is simply: print this string of random letters. And that makes the program long.

So a string of letters from a novel and a string of random letters of the same length might both have high algorithmic complexity — even though one is gibberish, and the other tells a story.

We want to be able to say the novel is more complex than the random string. There’s something about the way the letters are arranged that gives the novel meaning —something the random string doesn’t have.

So, there’s a bit of a problem algorithmic complexity. It can’t seem to differentiate between randomness and emergence.

Maybe we need a different approach. Maybe we need to ask when and where complexity arises.

Q2: Where Does Complexity Come From?

Let’s start somewhere that might feel a little unexpected: with a grid of black-and-white squares.

Have you heard of Conway’s Game of Life?

It’s a simple computer program that plays out on a grid of black and white squares. Each square on the grid follows a simple set of rules: it is born, it dies, or it hangs on for another round, depending on what its neighbours are up to.

I know — it’s a long way from brains and apple trees — but as it turns out, these simple systems, called cellular automata, have become a favourite tool for people who think a lot about complexity.

If cellular automata are new to you, I put together a short explainer earlier this year that might help. And if you’d like to see the Game of Life doing its thing, our friend

Wyrd Smythe

has a great playlist of examples. Here’s one to start with:

One person who’s spent a lot of time thinking about these systems is Stephen Wolfram— a physicist and computer scientist who spent many years exploring cellular automata. He focused on a particular kind: one-dimensional grids with very simple rules. He gave each rule a number — like Rule 30 or Rule 110 — and then just… let them run.

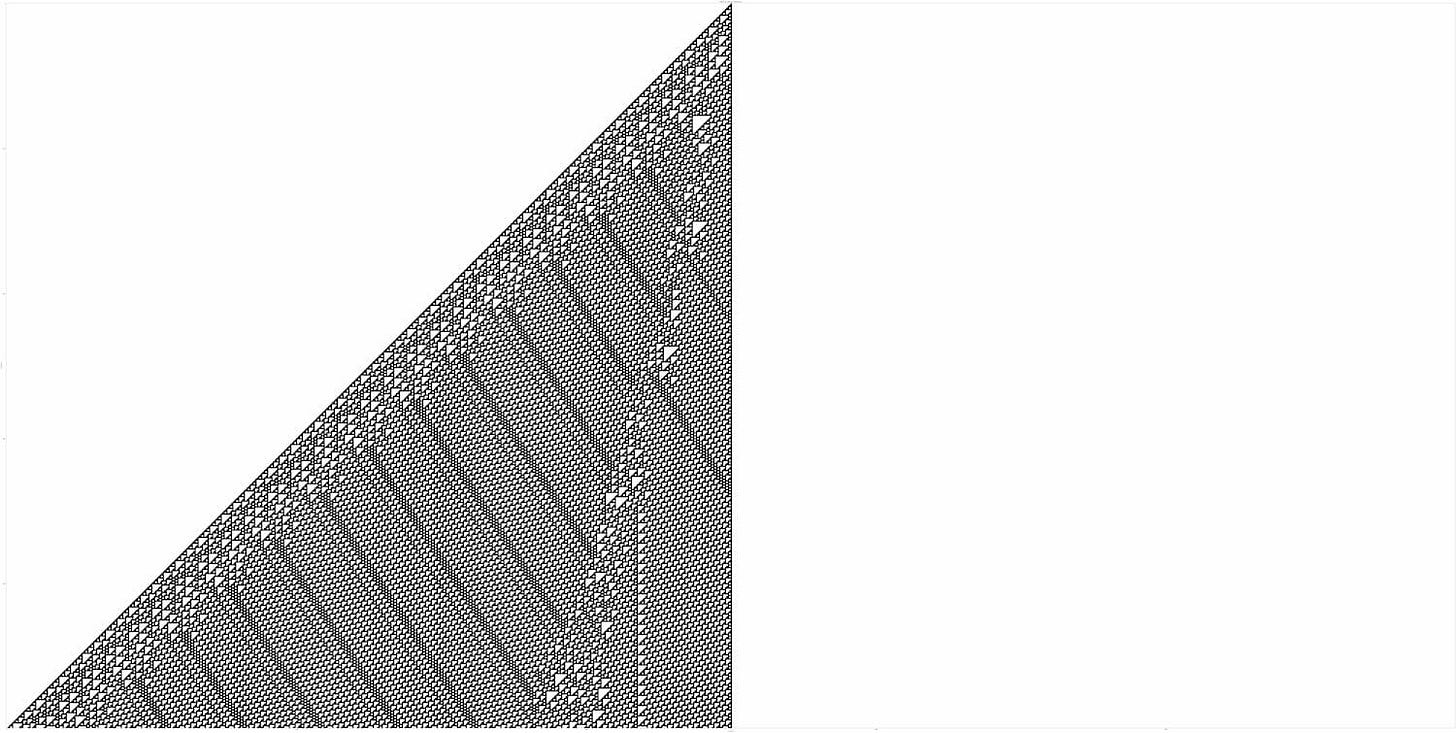
The setup is always the same: you start with a single black square at the top of the grid. Each row that follows depends on the row before it. And the rules are very simple —something like: if a square is black and both its neighbours are black too, then in the next row, that square turns white.

Here’s the set of rules for Rule 110:

And this is how it would play out in the first 5 rows:

Here’s what Rule 110 looks like after 500 steps:

It’s a patterns that has structure, but it’s also not quite regular. It’s orderly, but also unpredictable.

Rules like 110 — rules that produce patterns that look complex — are rare. Most of the rules either don’t do much at all, or they spin out into what looks like chaos. That contrast — the fact that simple rules can lead to such different outcomes — is what caught the attention of Wolfram. He began grouping cellular automata into four broad classes, based on how they behave over time.

• Class 1: systems that quickly settle into a frozen, uniform state.

• Class 2: systems that repeat in neat little loops — orderly and predictable.

• Class 3: systems that spiral into chaos — disorderly and unpredictable.

• Class 4: systems that create intricate patterns. Like Rule 110.

What’s interesting about Class 4 systems is that they look complex to us. They are, in a sense, apparently complex.

So, can we measure that? Can we quantify complexity in a way that reflects how it appears to us?

2️⃣ Apparent Complexity

(is our second measure of complexity)

Earlier, we saw that algorithmic complexity doesn’t quite capture what we mean by complexity — it can’t tell the difference between something that looks richly structured and something that’s just random noise.

Complexity is hard to define, but we often feel like we know it when we see it.
Scott Aaronson, Sean Carroll, and Lauren Ouellette wanted a way to capture that kind of complexity and express it mathematically.

To do this, they looked at how cream mixes into coffee. If we start with cream-on-top coffee we have an ordered state — cream particles on top, coffee particles on the bottom. If we mix the coffee we eventually get equilibrium: where all the coffee and cream particles are evenly mixed (a disordered state). It’s between the cream-on-top state and the mixed state when coffee looks most complex. Swirls and tendrils of cream stretch through the coffee.

To try to measure this apparent complexity, they generated digital images of coffee at different stages of mixing. Then they coarse-grained the images — which is just a fancy way of saying they blurred the images (You could still tell what state the coffee was in — just with the fine grained detail was softened.) Finally, they compressed the resulting images using a standard file compressor like gzip.

They used the file size of the compressed image as a proxy for apparent complexity. Images with fewer details compress into smaller files; those with more structure or variation compress into larger ones.

This approach is similar in spirit to algorithmic complexity. But by blurring the images, they weren’t analysing every pixel of fine-grained detail — they were trying to capture the larger patterns that we associate with apparent complexity.

And they found that file size does a surprisingly good job of measuring apparent complexity.

You can try a version of this yourself. Next time you have a coffee with cream sitting on top, take a photo of it. Then, start mixing your coffee, and take another photo as the swirls begin to form. The file size of the swirled photo will be larger than the cream-on-top photo.

📌 Let’s put a pin in whether apparent complexity is a good measure — we’ll come back to that question a bit later.

But first, I want to focus on something else about Carroll and Aaronson’s experiment — the idea that complexity seems to live in the in-between. Between order and disorder.

The Relationship Between Complexity and Entropy

Let’s consider cream-on-top coffee. It’s orderly — a low-entropy state. And it’s also fairly simple. Fully mixed coffee, on the other and, is disorderly — a high-entropy state. But note that, like cream-on-top coffee, mixed coffee is also simple.

It’s that in-between stage — when the cream is stretching into tendrils and swirling through the coffee — where we see complexity.

So on an entropy scale coffee goes from order to disorder. But on a complexity scale coffee go from simple to complex to simple.

The relationship between entropy and complexity can be seen in other things too. Right after the Big Bang, the universe was in a low-entropy state—ordered, and simple.³ The stars and galaxies hadn’t formed yet.

If we jump to the end of our universe — far, far into the future — entropy will eventually reach a maximum — a state of equilibrium. Physicists call this —

The heat death of the universe. (They’re not exactly known for their charm, those physicists.)

This final state will be a disordered high entropy state, yes. But it will also be simple.

It’s now — this moment in between — when entropy is rising, that complexity happens.

Galaxies form. Stars burn. Planets spin into orbit. And life happens.

Complexity seems to exist in the in between.⁴

It turns out Carroll and Aaronson weren’t the first to notice that complexity seem to exist in the in between.

Back in the 1980s, around the time Wolfram was classifying his cellular automata, American computer scientist Chris Langton began wondering: why do some of Wolfram’s rules lead to simplicity, others to chaos, and only a rare few to complexity?

Each of Wolfram’s rules is made up of eight instructions. He noticed that some rules were very active — most of the eight instruction turned cells on in the next row (like Rule 254).

Others were mostly inactive — they mostly turned them off (like Rule 1).

So he figured out a way to measure how active a rule is.

3️⃣ He called this parameter lambda, written with the Greek letter λ.

(this is our third way to quantify complexity)

A rule that turns every cell off has λ = 0. A rule that turns half of them on has λ = 0.5. Langton ran simulations across a range of λ values to see what would happen.

At low values, systems fizzled out into nothing much (Class 1). Nudge λ up and you get repeating loops (Class 2). Push it further — toward 0.5 — and chaos erupts (Class 3).

But right in between — clustered around λ ≈ 0.27 — Langton found Class 4. Complexity. Rules like the Game of Life and Rule 110. .

Langton had stumbled onto a kind of Goldilocks zone. Not too rigid. Not too random.

He didn’t call it the Goldilocks zone, though. He called it —

The edge of chaos.

(again with the charming names.)

✌️ The edge of chaos is the second hallmark of complexity.

It’s a big deal in complexity science because it’s where complex, emergent behaviour tends to appear. Weather systems, traffic patterns, economies — even stock markets — all hover near that edge, where order and disorder are constantly in tension.

This all sounds perfectly reasonable — until someone leans in and asks: Wait...

Is this really what we mean by complexity?

Rule 110 looks more complex than Rule 1, and swirling cream in coffee looks more complex than fully mixed coffee. This all feels true.

Rule 1

But if we define complexity by saying we know it when we see it, and then we use that definition to study how and when complexity occurs… the whole approach starts to seem rather circular.

📌 Let’s return to that idea we pinned earlier — apparent complexity. Apparent complexity is one attempt at a more objective approach. It tries to quantify how complex something looks once you’ve blurred away the fine details by measuring file size.

But even apparent complexity smuggles in our assumptions about what matters. The method we choose to blur and compress images will reflect what we think is important. We tend to choose techniques that preserves the features we care about. So in the end, the measure risks reinforcing our definition of complexity.

As you can see, quantifying complexity is tricky⁵.

But there’s another issue, too.

Cellular automata don’t capture everything we mean when we talk about complexity.

When we say a tree is complex, or a bird is complex, or the brain is complex, we’re pointing to something that cellular automata don’t fully express.

We might say that Rule 110 and a human are both complex — they both show the first two hallmarks of complexity: they have emergent properties, and they exist at the edge of chaos. But only one of them learns, makes predictions, self-organises, and adapts to its environment.

Only one of them keeps complexity going.

🤟 Which brings us to the third hallmark of complexity…

Q3: Is Life a Special Kind of Complexity?

Some systems, like weather patterns, seem to end up at the edge of chaos by accident. They drift into that zone where order and disorder balance — and then drift right back out. There’s no built-in mechanism holding them there.

But life seems to stick around. Life seems to have evolved to stay at the edge of chaos.⁶

If a creature becomes too rigid — too fixed in its behaviour or too specialised for a narrow niche — it can’t adapt when conditions change. A sudden drought, a new predator, or a shift in climate — and it’s going to struggle to survive.

On the other hand, if a creature is too unstable — too random, too chaotic — it might forget to eat, fly toward predators, or lay eggs in the snow. Creatures like that don’t last long either.

But right at the edge — where organisms are flexible enough to explore new possibilities, yet stable enough to preserve what works — that’s where life finds its sweet spot.

Theoretical biologist Stuart Kauffman found that systems capable of change — systems that process information, respond to feedback, and adapt over time — tend to self-organise in a way that pushes them right up to the edge of chaos and holds them there.

The edge of chaos is the perfect place for life.⁷ It offers the maximum diversity of behaviour without sending it into chaos.

This idea — that life doesn’t just sit at the edge of chaos, but builds scaffolds to stay there — echoes something Erwin Schrödinger hinted at in his famous book What Is Life? He saw life as a system that feeds on order to resist disorder. A structure that maintains complexity in a universe that’s always trying to pull it apart.

This might be why life, as we know it, is the most complex thing in the known universe. Not just because it emerges, and not simply because we find it at the edge of chaos — but because it has figured out how to stay there.

All these words — complexity, emergence, life, and adaptation — are things we are only just starting to figure out. There’s still a tone of work to do, but that’s what makes complexity science one of the most exciting frontiers in modern science.

Next Week…

Let’s turn to the question lurking underneath all this: is complexity enough to explain consciousness?

1. ...though what we mean by simple depends on the lens we use — math, physics, or computation.

2. If you're looking for more formal definitions of complexity from math and computer science, here are some key resources:

• Kolmogorov, A. N. (1965). Three approaches to the quantitative definition of information. Problems of Information Transmission, 1(1), 1–7.

• Chaitin, G. J. (1966). On the length of programs for computing finite binary sequences. Journal of the ACM, 13(4), 547–569.

• Solomonoff, R. J. (1964). A formal theory of inductive inference. Part I. Information and Control, 7(1), 1–22.

• Bennett, C. H. (1988). Logical depth and physical complexity. In R. Herken (Ed.), The Universal Turing Machine: A Half-Century Survey (pp. 227–257). Oxford University Press.

• Gell-Mann, M., & Lloyd, S. (1996). Information measures, effective complexity, and total information. Complexity, 2(1), 44–52.

• Sipser, M. (2012). Introduction to the theory of computation (3rd ed.). Cengage Learning.

• Langton, C. G. (1990). Computation at the edge of chaos: Phase transitions and emergent computation. Physica D: Nonlinear Phenomena, 42(1–3), 12–37.

3. While the early universe had high thermal entropy, it had low gravitational entropy — which is why many physicists consider it a low-entropy state overall. But this framing is still debated.

4. Many complex systems appear to exist between order and disorder, but this is a phenomenon that is still under active investigation.

5. Fellow Substack writer and neuroscientist

Erik Hoel

has just released a new paper on his updated theory of emergence. It’s called Causal Emergence 2.0: Quantifying Emergent Complexity, and it’s a fascinating attempt to quantify emergent complexity across scales. I may come back to it in a future piece.

6. This remains a hypothesis rather than a settled scientific fact.

7. Some theories propose this, though not all biologists or physicists agree.

---