Having All The Information Isn't The Same As Knowing Everything
How does simplicity give us immense complexity?
If you are new here, welcome!
If you’ve been around for a while, you know I love exploring the fascinating intersection of neuroscience, consciousness, and AI. Typically, I do this by writing in-depth essays. But for the start of 2025, I thought we could try something different — a series of shorter pieces to spark our curiosity.
Six questions have been tugging at my thoughts. I’d like to share these questions with you through a mini-series of mini-essays. Think of them as conversation starters — I’ll dive deeper into each one throughout the year ahead.
This is Question 2
Over the holidays, I played pool with my nephew. As is often the case when we play, the game quickly turned into a conversation about tactics.
‘So, Aunty Suzi, you’re saying I can use geometry and physics to predict where the ball will go?’
‘Exactly! Hit the ball right here, with just the right amount of force, and it’ll go straight into that pocket. Its path is perfectly predictable — it’s just the rules of physics!’
‘Okay... but what about when I break the rack at the start of the game? Each ball in the rack follows those same rules of physics, right? So why can’t I predict where all the balls will end up after I break?’
My nephew asks excellent questions!
We tend to think that if something follows clear, deterministic rules, we should be able to predict exactly what it will do. After all, that’s how we can forecast solar eclipses centuries in advance or calculate the precise trajectory of a spacecraft to Mars.
This intuition about predictability is so strong that many people believe if we just had enough computing power, we could predict everything that follows simple rules — like where all the balls will end up on a pool table.
But, it turns out, this might not be true. Something fascinating happens when simple rules interact over and over again.
Have you heard of Conway’s Game of Life? It’s a simple, rule-based game that illustrates a fascinating idea called
Cellular Automata.
(Stick with me; this gets really interesting!)
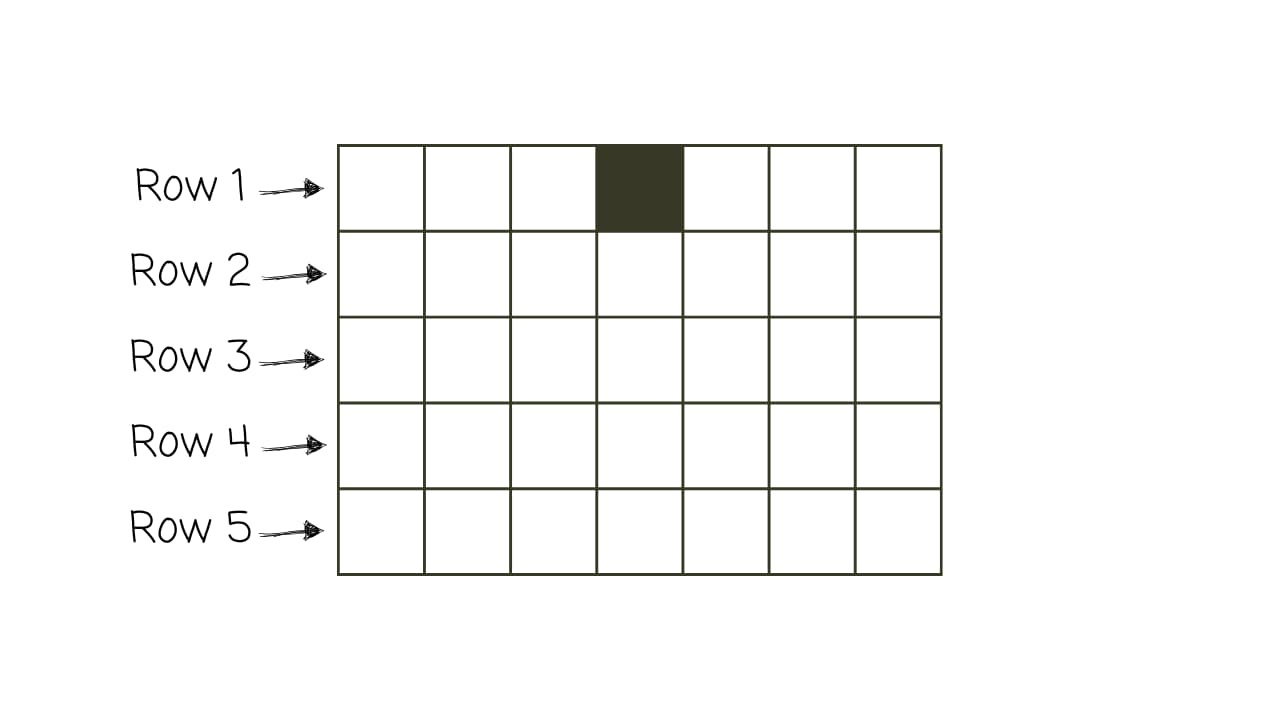
Imagine a simple grid where each square can be either black or white. Think of each row on the grid as a new generation.
The squares in each row change colour based on the row before it and a set of simple rules. For instance, a square in the next row might turn white if, in the current row, it’s black and its two neighbours are also black.
Each type of cellular automaton follows its own unique set of rules — simple instructions applied over and over again.
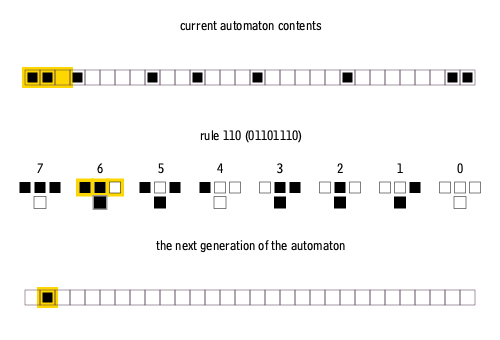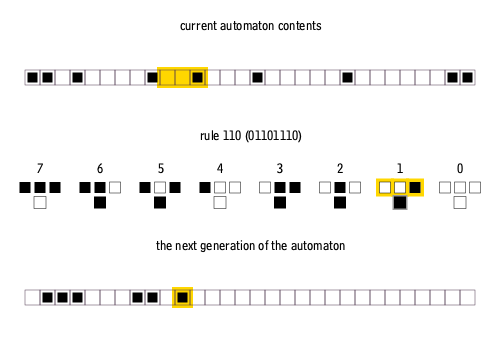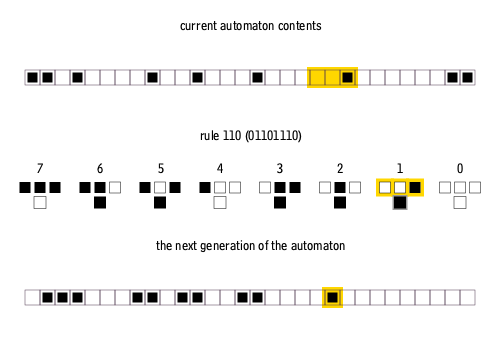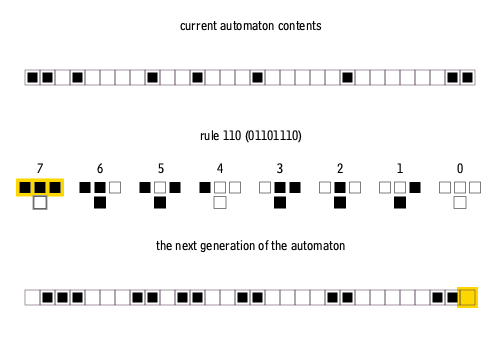
Here’s an example in action: the set of rules for Rule 110 (Stephen Wolfram, 2003), a particularly interesting cellular automaton.
If we start in row 1 with just a single black square in the centre, Rule 110 would unfold like this:
At first glance, you might expect such simple rules would produce boring, repetitive patterns. But let’s simulate Rule 110 for 100 steps:
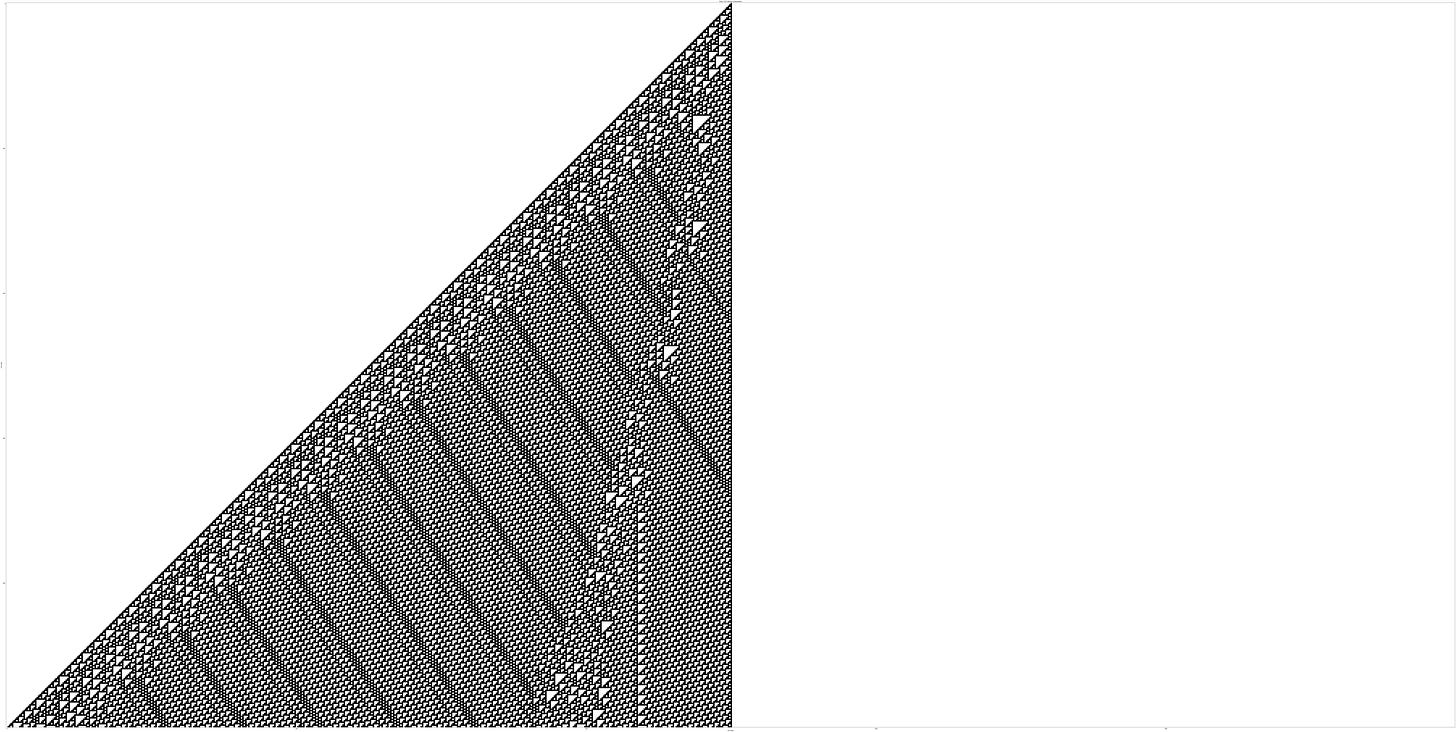
Now, extend it to 500 steps:
We start to see something remarkable: a mixture of stability and chaos. Some regions of the grid show orderly, predictable patterns, while others appear entirely random and unpredictable.
Two things stand out to me about cellular automata, like Rule 110.
First, we don’t need complex rules to create complexity. Even the simplest rules, when applied repeatedly, can give rise to patterns of staggering intricacy.
Second, and perhaps more surprising, is this: even though we know the rules of Rule 110, there’s no way to predict what will happen next without running the process itself. The pattern isn’t predictable from the outset. There are no mathematical shortcuts or neat formulas. If you want to know what row 753 will look like, you have to run the simulation step by step. The computation is the shortest path to the answer.
The idea that the only way to know the answer is to run the simulation isn’t unique to cellular automata — it’s a phenomenon that shows up in many complex systems.
Take weather patterns, for instance. Even with the most powerful supercomputers and detailed atmospheric models, we can’t reliably predict the weather more than a few days ahead. This prediction requires running a simplified simulation. And even then, tiny uncertainties quickly compound over time. A slight variation in initial conditions, or a tiny tweak to our assumptions, can lead to dramatically different outcomes. It’s the famous butterfly effect: the idea that the flap of a butterfly’s wings in one part of the world could set off a chain of events leading to a hurricane in another.
We see this same principle in biology. DNA is a remarkably simple code — just four chemical letters, A, T, C, and G, arranged in sequences. But even if we know the complete genetic sequence of an organism — say, a tree — there’s no way to predict the tree’s final shape just from the sequence. The only way to know is to let the tree grow.
This is the information problem. Even when we know all of the information — that is, even when we know all the rules and the current state of the world — we still don’t know everything. Even with complete knowledge of the current state of a system — whether it’s the weather, a tree, or the position of particles — it seems we can’t always predict what will happen next. Sometimes, the only way to know is to let the process unfold.
I find this fascinating. So, the second question on my list of questions for 2025 is:
How do simple, deterministic rules lead to unpredictable complexity?
An interesting aside:
One key difference between cellular automata like Rule 110 and biological systems is that no matter how many times you run Rule 110, it will always produce the same results. This is not true for trees. Trees and other biological systems are influenced by their environment. No two trees have the same environment, which means no two trees will ever grow in exactly the same way.
Unlike a tree, Rule 110 doesn’t interact with an external environment — its complexity arises entirely from its internal rules. And yet, even without environmental interactions, Rule 110’s simple rules can generate complexity.
This is intriguing. While interaction with the environment often adds complexity to a system, it seems that we can get complexity merely from the unfolding of a simple set of rules.








You very effectively demonstrate how a single, simple system can generate unexpected complexity. Now imagine stacking multiple complexity-generating systems into layers operating at different scales:
- one angstrom, molecules
- one micrometer, cell biology
- 100 micrometers, neurons and glia
- 1 millimeter, cytoarchitecture (attractor networks, etc)
- 1 centimeter, maps (Brodmann areas, entorhinal cortex, etc.)
- 10 centimeters, systems (cerebral cortex, hippocampus, etc.)
- one meter, central nervous system
- one meter to many kilometers, society, culture, Internet...
The potential complexity boggles the mind. It is also the reason I have a hard time with reductionism - the idea that you can understand the whole if you first understand the parts. Reductionism has served science well for hundreds of years but it has failed to penetrate a multi-layered system as complex as the human brain.
Nice essay. I first met Conway’s game properly via William Poundstone’s small book on complexity. Then I played around with it in the environment on old computers with (very inefficiently) Algol60, as it was all I knew and had access to a compiler for. Great memories AND complexity theory with no maths! I do enjoy these weekly posts and love the way you hook your audience into areas that I’m pretty sure they wouldn’t necessarily connect with recreationally - it has a nice integrated cross-disciplinary vibe. Bit like physiology used to have for me (no expert, just a fan of the discipline). Thank you yet again :)