Information Isn't Free. Even Demons Must Pay

Information and Complexity: Essay 3

Your brain is an information processor.

That’s how we tend to think about it, anyway.

It takes in signals, sorts them, stores them, recalls them when needed. Right now, as you’re reading this, your brain is translating shapes on a screen into words, connecting them to ideas, predicting where this is going.

We navigate the world by processing information.

But hold on. What do we actually mean by information? We use the word all the time, but do we ever stop to think about what it is?

Given how central information is to the topics we explore in this newsletter — artificial intelligence, neuroscience, and consciousness — getting a clearer picture of what we really mean by information is necessary.

In the last essay, I talked about Information Theory — the mathematical framework pioneered by Claude Shannon. This is the kind of information that powers the internet, telecommunications, and even AI.

Information Theory is certainly one way to define information. But it’s not the only way.

Physics talks about information too. And when physicists talk about information, they mean something — physical.

Information in Information Theory and information in physics seem to have little to do with each other. One belongs to the world of communication and computation, the other to the fundamental laws. They seem to be speaking different languages.

But appearances can be deceiving.

There’s a famous problem in physics that hints at a deeper connection between the two.

(This is where things get weird.)

In 1867, physicist James Clerk Maxwell dreamed up a tiny demon. A creature that could seemingly break the rules of physics. And for over a century, some of the brightest minds in science tried to outsmart it — and failed.

The puzzle — now known as Maxwell’s Demon — was a problem in physics. But the answer came from — Information Theory.

Why?

What does information, a concept born in the age of telegraphs and computers, have to do with the fundamental laws of the universe?

The answer lies in entropy.

Entropy?

Wait. What?

Isn’t entropy just another word for disorder? What does that have to do with information?

Turns out, quite a lot, actually.

To find out why, let’s explore three questions:

1. What does physics have to say about entropy?

2. What is the puzzle that stumped physicists for over a century?

3. How was the puzzle solved — and what does that tell us about information?

---

Before we get to Maxwell’s Demon, we need to take a quick pit stop at —Information Theory.

Why? Because it will help us understand why the demon puzzled physicists for so long.

In Information Theory, information is all about surprise. The more unpredictable something is, the more information it carries.

Think of it this way: If I tell you the sun will rise in the east tomorrow, you haven’t learned much. But if I tell you the sun will rise in the west… well, that’s a lot of information.

The cool thing about information in Information Theory is that we can actually measure information.

The unit of measurement? It’s the humble bit.

A single bit is the amount of information you get from a yes-or-no question. Flip a fair coin — heads or tails? That’s one bit of information.

But what if I pick a random card from a shuffled deck? Now, instead of just two options, there are 52. That means when you flip over one card, you gain about 5.7 bits of information.

In information theory entropy is defined as the average amount of information or uncertainty associated with a random variable.

That’s really all you need to know about Information Theory for this essay.

But if you’re the kind of person who actually wants to calculate the information content of a coin toss in excruciating detail (no judgment — I’m one of those people), I’ve put together a primer on the math.

Q1: What Does Physics Have to Say about Entropy?

In Information Theory, entropy is fairly easy. It’s a number. A value you can calculate. No ambiguity.

But in physics? Entropy is… slipperier.

Entropy is one of the most fundamental ideas in science. It explains a lot — from why coffee cools to why time only moves forward.

But it’s also one of the most misunderstood.

To understand the puzzle Maxwell posed, we don’t need to master everything about entropy. We just need to focus on two key definitions of entropy — and one fundamental law of physics.

Two Definitions of Entropy

Definition 1: Entropy as Disorder

If you remember entropy from high school, you probably heard it described as disorder.

You might have been told that a messy room has high entropy. And a tidy room has low entropy. Seems simple enough, right?

But although disorder is a helpful shorthand for thinking about entropy, it’s not quite right. Physicists prefer a different definition — one that explains entropy with more precision.

Definition 2: Entropy as the Number of Possible Arrangements

Ludwig Boltzmann, one of the great pioneers of statistical mechanics, gave us a better way to think about entropy.

Forget disorder. Instead, think of entropy as

the number of ways something can be arranged while still looking the same at a larger scale.

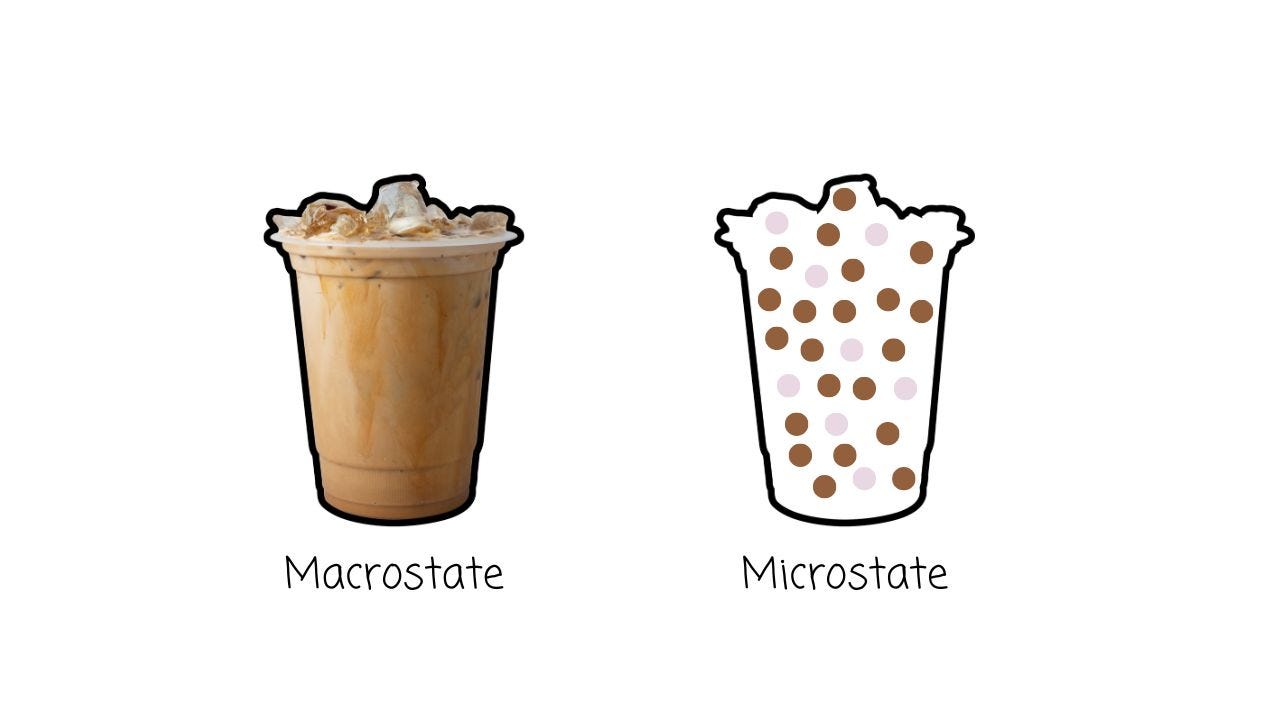
Let’s break that down with a cup of coffee.

Imagine you pour cream into your coffee. At first, it sits in a neat layer on top. That’s the macrostate — the big-picture description.

But if we zoom in, we see the microstate — the countless tiny molecules of coffee and cream.

Now, think about all the different ways those molecules could be arranged.

Some of those arrangements will give us a nice, separated layer of cream-on-top coffee. But many, many, many more will give us something else: fully mixed coffee.

So, we say that mixed coffee has higher entropy than cream-on-top coffee — because compared to cream-on-top coffee, there are way more ways for mixed coffee to exist.

---

This brings us to one of the most famous laws in physics:

The Second Law of Thermodynamics

You’ve probably heard it before — entropy always increases.

But why does it increase?

If you understand the second definition of entropy, the answer is fairly simple — high-entropy states are overwhelmingly more likely than low-entropy ones.

Imagine you take a brand-new deck of cards, perfectly arranged in order.

Now shuffle it.

What are the odds that, by sheer chance, you’ll shuffle it back into perfect order?

Virtually zero.

There’s only one way for the deck to be ordered, but countless ways for it to be unordered (or random). A randomly shuffled deck is simply much more likely than a perfectly ordered one.

The second law explains many everyday phenomena: logs burn to ash but ash never reassembles back into a log, sugar dissolves in water but never crystallises back into a cube, and eggs break but never unbreak.

Technically, the laws of physics don’t forbid an egg from unbreaking.

It’s just… breathtakingly unlikely. If we did the math it would be something in the order of 1 in 10 to the power of 150 billion trillion.

But could there be a loophole?

Could there be a system that — against all odds — seems to defy the Second Law?

Maxwell wondered that too.

Q2: What is the Puzzle That Stumped Physicists for Over a Century?

By 1867, physicists had made peace with the Second Law of Thermodynamics. Entropy always increases.

But then, James Clerk Maxwell had an idea. A provocative idea.

What if… there was an exception?

He imagined a tiny creature that, in theory, could cheat the Second Law. This seemingly simple idea was so perplexing, it haunted physicists for over a century.

We now call it Maxwell’s Demon.

Here’s how it works

Imagine a box filled with gas molecules bouncing around randomly. Over time, those molecules spread out evenly. No part of the box will be hotter or colder than any other. All good so far — that’s exactly what the Second Law predicts.

But now, let’s mess with that.

Divide the box into two chambers, separated by a tiny, frictionless door. And put our demon in charge of that door.

The demon watches the gas molecules very carefully. It knows that heat is just molecules in motion — hot molecules move fast, cold molecules move slow.

So, the demon gets to work.

• Whenever a fast-moving (hot) molecule approaches from the right, the demon quickly opens the door, letting it pass into the left chamber.

• Whenever a slow-moving (cold) molecule approaches from the left, the demon opens the door to let it into the right chamber.

Over time, the left chamber fills with fast molecules — hotter gas. And the right chamber fills with slow molecules — colder gas.

The demon has separated the hot and cold molecules.

It’s created order from disorder.

It’s reversed entropy.

It’s defied the Second Law of Thermodynamics.

That… should be impossible.

Where’s the Catch?

In the real world, reducing entropy always comes at a cost.

A refrigerator keeps food cold — but it does so by consuming electricity and releasing heat. A steam engine converts heat into motion — but only by burning fuel and releasing waste energy.

If you want to decrease entropy in one place, you must increase it somewhere else.

So… if the demon is actually lowering the entropy of the gas, where is the cost?

It can’t be from opening and closing the door — Maxwell specifically imagined it as frictionless, requiring no energy at all.

For over a century, no one could answer this paradox.

Physicists believed the Second Law was… well law. Unbreakable.

And yet, Maxwell’s Demon was suggesting he could.

Eggs break, but don’t unbreak.
Hot coffee cools, but doesn’t reheat itself.
And gas molecules don’t separate on their own — unless there’s a cost.

So where was entropy sneaking back in?

Where was the hidden price?

Q3: How Was the Puzzle Solved — And What Does That Tell Us About Information?

Physicists were convinced that Maxwell’s thought experiment had to be wrong.

But for decades, no one could say why.

Then, in 1929, a Hungarian physicist named Leó Szilárd took a new approach. Like others, he suspected the demon must be paying a thermodynamic cost. But he had a hunch the cost wasn’t obvious.

So he ran the numbers. And he found something surprising. Each time the demon makes a decision—choosing whether to let a molecule through—it gains one bit of information about the system.

One bit.

As in Shannon information.

The same fundamental unit that underpins modern computing. A simple choice between two possibilities: fast or slow, left or right.

But in 1929, acquiring information wasn’t considered work. Information was just an abstract concept—mathematical, not physical.

And that was the key. Szilárd’s insight suggested something radical: information isn’t free.

Somehow, gathering information has a hidden energy cost.

Let’s take a moment to appreciate just how strange this is.

We started with the idea that thermodynamic entropy and Shannon entropy belonged to completely different worlds.

One describes heat and disorder in physical systems. The other describes messages, bits, and uncertainty in communication. But this century-old problem in thermodynamics seemed be about bits — Shannon information.

What Szilárd was suggesting was profound: information has physical consequences.

But how?

That mystery remained unsolved for another 30 years.

---

In 1961, a physicist at IBM named Rolf Landauer made a crucial realisation. For the demon to keep functioning — to sort molecules forever — it must eventually erase old information to make room for new measurements.

And erasing information, Landauer discovered, is a physical process. A process that releases heat and increases entropy. This was the missing entropy.

It wasn’t in the demon’s movements.

And it wasn’t in the frictionless door.

It was hiding in the cost of erasing information.

The demon wasn’t cheating the Second Law.

To tie this all together, we need one last definition of entropy.

Definition 3: Entropy and Energy

Entropy is sometimes described in terms of energy, but it’s not actually energy.

Rather,

entropy measures how much of a system’s energy is unavailable for useful work.

Physicists love closed systems — systems where no energy is added or removed.
Maxwell’s box of gas molecules is one of these systems.

The key thing about closed systems is that their total energy never changes.
That’s the First Law of Thermodynamics.

But while the total energy stays the same, what does change is how much of that energy is useful.

A charged battery is an example of low-entropy energy—energy that’s ready to do work. As the battery is used, that energy isn’t lost, but it becomes less useful, spreading out as heat. Entropy increases.

And that’s exactly what happens when the demon erases information.

To keep sorting molecules, the demon has to gather information about the movement of the molecules. And eventually, it has to erase old information to make room for new information. And that’s when the price is paid.

Each time the demon erases a bit of information, it releases heat — converting useful, low-entropy energy into less useful, high-entropy energy.

That’s where the missing entropy was hiding all along.

The second law wins.

Landauer had solved the puzzle.

Information processing isn’t free — it has real, physical consequences.

At least, that’s the mainstream view.

As always, the conversation doesn’t end.

Maxwell’s Demon may have been defeated, but some lingering questions remain. And in the spirit of intellectual honesty, let’s take a moment to acknowledge some of them.

Are Information and Thermodynamic Entropy Really the Same Thing?

The math is strikingly similar. Both Shannon entropy (from communication theory) and thermodynamic entropy (from physics) follow the same fundamental equations. They both describe uncertainty, randomness, and constraints on what’s possible.

But are they fundamentally connected? Or is the overlap just a coincidence—a mathematical trick that happens to work in both worlds?

Most physicists believe the connection runs deep. But some remain unconvinced.

Did We Really Defeat the Demon?

For most scientists, Szilárd and Landauer gave us the final answer. Maxwell’s Demon isn’t a loophole in thermodynamics — it just hides the cost of information processing.

But some critics, like John Earman and John D. Norton, argue that this explanation cheats. They claim Szilárd and Landauer’s arguments assume from the start that the Second Law of Thermodynamics must hold. Then, based on that assumption, they derive constraints — like the energy cost of erasing information — that justify why entropy always increases.

If that’s true, then the whole argument is circular reasoning.

They argue that instead of proving the Second Law, the argument just restates it in a more complicated way.

This isn’t a mainstream view in physics or information theory. But in the philosophy of physics, the debate isn’t entirely closed.

The Bigger Question: What Is Information, Really?

So far, we’ve treated information as something quantifiable, measurable, and tied to entropy and computation. Bits and data.

But… is that all information is?

When we talk about meaning, interpretation, and understanding, are we still talking about the same thing? Does the physics definition of information capture everything we mean by information?

Or is there something more?

Next Week...

Even with lingering uncertainties, the mainstream position in modern physics is clear: Information isn’t just an abstract concept — it has real, measurable effects in the physical world.

And if that’s true, it raises some big questions.

Think about it.

Every time you permanently delete a file — you’re not just managing information. You’re increasing entropy. If erasing information has a physical cost, what does that mean for systems that process information?

Computers process information.

So do brains.

Entropy might help us understand memory and thinking in machines — like AI, neural networks, and computation.

But what about us?

Next week, let’s get speculative.

If entropy is at the heart of information processing… then what else might it be responsible for? And what does this tell us about systems that think?