Is Consciousness Computational?

Could a computer running algorithms really have conscious experiences?

Hello Curious Humans!

Remember the movie Transcendence? You know the one where Johnny Depp plays a scientist who has his consciousness uploaded into a supercomputer? Don’t worry if you haven’t seen it — apparently, it was pretty rotten (Rotten Tomatoes: 19% 🤢)

Despite its flop at the box office, the movie’s plot revolves around one fascinating question — is our consciousness just a complex computational process?

Many in the AI and cognitive science community assume it is — which means, many believe that it might be possible to replicate or simulate consciousness in a machine using advanced algorithms and computing power.

Before we dive into some of the arguments for and against this idea, let’s first review the theory that underlies it.

Note: I will use the term mental states throughout this article, which is an annoyingly vague term, I know! Trying to write a clear definition is tough because people disagree about what they are. So, let’s not get tangled in that messy rabbit hole just yet. By mental states, I mean all the thoughts, feelings, perceptions, intentions, experiences, beliefs, desires, emotions, memories and all the other things you think about. We’ll dive into the definitional rabbit hole in another article.

Functionalism

At its core, functionalism is the idea that mental states (thoughts, feelings, perceptions, intentions, and possibly consciousness) should not be defined by what they are made of but, rather, they should be defined by the function or the role that they play. In other words, a mental state is more about what it does than what it is made of.

This concept can seem a bit abstract, so an analogy might help. We tell the time by looking at a clock. But a clock could be analogue — made of gears, springs, and pendulums — or digital, made of microcontrollers, LCD displays, and electronic oscillators. Telling time is best thought of as the function that a clock performs. And it's this function of telling time that's crucial, not the specific materials or components that perform that function.

Functionalism comes in different varieties; some views equate mental states with the functional roles themselves, while others link mental states to their physical states. In this article, I’m going to look at a specific type of functionalism called computational functionalism.

Computational functionalism agrees that mental states are defined by their functional roles, but it goes a step further by specifying that these roles are computational processes. It sees mental states as akin to software running on the hardware of the brain.

Computational functionalism, therefore, subscribes to the idea that mental states do not depend on any specific physical substrate (like the biological brain). Instead, they are substrate-independent. That is, mental states could (at least theoretically) be realised in different physical mediums, provided that the correct functions are produced.

---

In this week’s issue of When Life Gives You AI let’s:

Take a closer look at computational functionalism by investigating two common objections to the computational functionalist claims:

1. The inverted spectrum thought experiment, and

2. A quantum theory of consciousness

---

But first, let’s make sure we understand the claims that computational functionalism is making. The chain of reasoning looks something like this:

1. They start by suggesting that every mental state — that is, every thought, feeling, belief, or experience we have — plays a specific functional role. So all mental states are a type of functional state (M → F).

2. They also claim that consciousness is a type of mental state, therefore, just like all other mental states, consciousness is a type of functional state (Con → M).

3. Next, they claim that functional states operate in a way that we can map out and understand in detail, which means (at least in theory) we can compute them (F → C).

4. Together, these ideas come to the conclusion that because consciousness is a functional state, it is mappable, and it is something we can compute (Con → C).

So, if we were going to argue against the computational functionalist view, we might look for reasons why 1, 2 or 3 above are not true.

---

1. The Inverted Spectrum Thought Experiment

Imagine two people. Let's call them Alice and Bob. Externally, they both seem to react to colours in the same way. They stop at red lights, go at green lights, and so on. However, internally, their experiences of colours are different. What Alice experiences as red, Bob experiences as green, and vice versa. Their colour experiences are inverted relative to each other.

According to functionalism, if two beings (like Alice and Bob) have the same functional responses to stimuli, they should have the same internal experiences. But the inverted spectrum hypothesis suggests that it's possible for two people to have the same functional responses (e.g., both stopping at red lights) while having different internal experiences (seeing different colours).

Implications for Computational Functionalism

If we take seriously the challenges posed by the inverted spectrum thought experiment, we might start to question the soundness of the computational functionalist view.

Let’s review the logic of the computational functionalist view:

1. Premise 1 (P1): All mental states are functional states. (M → F)

2. Premise 2 (P2): Consciousness is a mental state. (Con → M)

3. Premise 3 (P3): All functional states are computable. (F → C)

4. Conclusion (C): Therefore, consciousness is computable. (Con → C)

It seems we have a problem. Premise 1 and Premise 2 cannot both be true if consciousness is not a functional state.

• If consciousness is a mental state (P2), and if mental states include experiences that aren't captured purely by functional states, then not all mental states (including consciousness) are purely functional states (contradicting P1).

• Alternatively, if we insist that all mental states are functional states (P1), then consciousness, which cannot be accounted for by a functional description, might not fit into the category of mental states as defined by P1 (contradicting P2).

If that all sounds too confusing, just know that we are left with the conclusion that consciousness is not a functional state, and if consciousness is not a functional state, then according to P3, it's not necessarily computable.

BUT!! Let's not jump to that conclusion too quickly.

If we decide to reject computational functionalism based on the arguments raised by the inverted spectrum thought experiment — we better be sure that the thought experiment articulates a scenario that is actually possible. To do that we need to review the concepts of conceivability and possibility.

A Note about Conceivability

Thought experiments ask us to conceive of a situation that is beyond our experiences. In philosophy, conceivability is linked with possibility. However, the link between conceivability and possibility is used in different ways.

1. Conceivability as logically possible

The first way we use conceivability is to say that something is conceivable if we can imagine it without encountering any logical contradictions, even though it might not exist in our world. For example, when we watch the movie Star Wars, we can imagine Han Solo's ship, the Millennium Falcon, travelling at the speed of light because, in the Star Wars movie, spaceships exist that can travel at (or faster) than the speed of light.

The logical argument might go something like this:

1. Premise 1 (P1): Spaceships in the Star Wars universe are equipped with hyperdrive technology.

2. Premise 2 (P2): Hyperdrive technology allows for faster-than-light travel by propelling spaceships into hyperspace, where the constraints of normal space-time do not apply.

3. Conclusion (C): Therefore, spaceships in the Star Wars universe can travel at the speed of light (or faster) due to their hyperdrive technology.

This argument is logically valid — the conclusion logically follows the premises. But this sort of argument doesn’t tell us anything about the real world. It’s logically possible, but not necessarily physically possible in our world.

2. Conceivability as logically and physically possible

The second way that we use conceivability is to say that something is conceivable if it is logically possible AND it is physically possible in our world given the laws of physics.

For example, while we might be able to imagine spaceships travelling at the speed of light in Star Wars and lay out a logically valid argument for their possibility, light-speed travelling spaceships are not physically possible in our world.

If the Millennium Falcon travelled at the speed of light in our world, it would, at some point, be dragged into a black hole. To avoid this fate, it would need to travel faster than the speed of light (indeed, Solo claims his ship can travel faster than the speed of light in the movie A New Hope). But, in our world, travelling faster than the speed of light is not possible (or it encounters serious space-time-related problems).

---

Thought experiments, like the inverted colour spectrum, require us to conceive of a scenario that doesn’t actually exist in our world. When we do this, it is important that we understand the type of conceivability that we need to use.

If we use the first type of conceivability — something is conceivable if it is logically possible — then we can’t say much about whether or not the thought experiment is physically possible in our world. If we want to make claims about our world, we need the second type of conceivability — logically possible and physically possible.

Because Star Wars is a movie, it only needs the first type of conceivability — it just needs to be logically possible. But, the inverted colour spectrum is trying to say something about what is possible in our world, so it requires the second type of conceivability — it needs to be logically possible and physically possible.

Some have argued that while the scenario outlined in the inverted colour spectrum thought experiment might be logically possible — that is, it is logically possible to imagine that someone can experience yellow when we experience blue — further scrutiny reveals that it is not physically possible.

So, let’s take a look at how colour vision works in humans, and test whether the inverted colour spectrum is physically possible.

How colour vision works

As you will recall from high school physics, what we see as colour is actually electromagnetic radiation within a certain range of wavelengths (see Figure 1). Wavelengths within this range (~400 nm to ~700 nm) stimulate certain cells in our retina. Wavelengths outside this range do not stimulate those cells, so we can’t see them.

Figure 1. By Original: Penubag Vector: Victor Blacus - Own work based on: Electromagnetic-Spectrum.png, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=22428451

When we are asked to conceive of an inverted colour spectrum, we need to ask what it is that we are being asked to conceive. Are we to conceive that our perception of the entire electromagnetic spectrum inverts, or just the wavelengths that we see? If we are to conceive that our perception of the entire electromagnetic spectrum inverts, then at what point does this inversion occur? Theoretically, the electromagnetic spectrum is continuous — there is no inherent upper or lower limit to the wavelengths or frequencies that exist.

Putting that aside (let’s just pretend there is some point at which the perception inverts), would this mean that some of us see electromagnetic radiation in some ranges, while others see electromagnetic radiation in other ranges? Surely we could measure this difference? What about radio waves? If our perception of the entire electromagnetic spectrum was inverted for some people, would those people see radio waves and hear colours? Or would sensitivity to different wavelengths also invert?

A perception inversion of the entire electromagnetic spectrum doesn’t seem to make much sense.

What about a perception inversion of just the visible part of electromagnetic radiation? Let’s review how the human eye works to see if this type of perception inversion seems more physically possible.

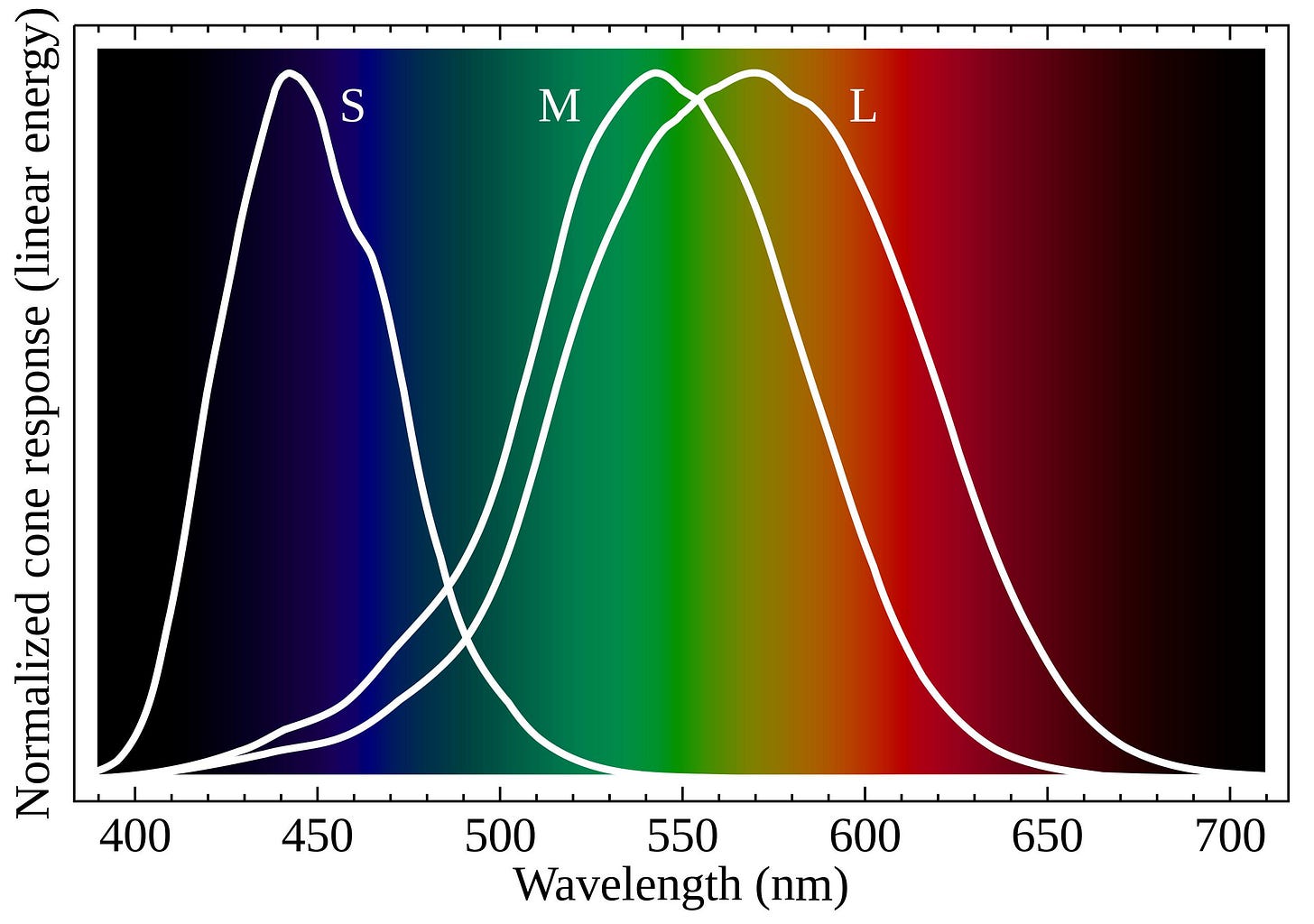
Most people with normal colour vision have 3 different types of cones in the retina: S-cones, which are sensitive to short wavelengths; M-cones, which are sensitive to medium wavelengths; and L-cones, which are sensitive to long wavelengths.

---

A cone is a type of cell (a photoreceptor) in the retina that's sensitive to colour and helps provide sharp, detailed vision in well-lit conditions. We use cones mostly during the day, when there’s lots of light.

In the retina, we also have rods — a different type of photoreceptor that's highly sensitive to light, which we use mostly at night or in other low-light conditions. Rods don’t discern color, so they don't contribute to color vision.

---

In Figure 2 (below) you can see three distinct curves — one for each cone type in the human retina. Each of these curves represents the range of wavelengths that they respond to. For example, S-cones respond mostly to wavelengths of light around 440 nm (which we see as blue).

Figure 2. BenRG, Public domain, via Wikimedia Commons

Our perception of colour can be described along three different dimensions —

1. hue (this is what we mostly think of when we think about colour),

2. luminance (we usually call this brightness), and

3. saturation (the intensity or purity of the colour)

Cone cells play a crucial role in all three of these dimensions.

Hue

In Figure 2 (above), you’ll notice that the activation of the M-cones and L-cones overlap considerably. This overlapping gives us greater sensitivity — or finer colour distinctions. This means we are able to distinguish between different hues better at wavelengths of light where M-cone and L-cone sensitivity overlap (green to red) than at the shorter wavelengths where the S-cones are sensitive (blues). And (perhaps as a result) we have more colour names (hues) for wavelengths of light within the M-L range.

Luminance

The perceived luminance, or brightness, of a colour, is influenced by how much it stimulates the M and L cones. For example, wavelengths of light in the 580 nm range (yellow) stimulate both M and L cones strongly, making yellow appear brighter than, say, blue.

Saturation

All three types of cones contribute to the perception of saturation. For instance, if S-cones are strongly stimulated (with minimal input to M and L cones), the perceived colour would be a highly saturated blue.

---

Understanding this, we might wonder whether a perception inversion of just the visible part of electromagnetic radiation should involve inverting all colour dimensions (hue, brightness and saturation) or just one dimension. If the perception inversion involves all colour dimensions, we might wonder whether this sort of perception inversion is a type of difference that makes no difference.

What if perception inversion only involves inverting the perceived hue, and perceived brightness and saturation remain uninverted? As cone cells play a crucial role in how we perceive hue, brightness, and saturation, some might argue that this sort of inversion is physically impossible. But, if it were possible, we might wonder what this would mean. Would some people perceive blue as brighter than yellow?

We could spend many head-in-hand hours trying to map different versions of the inverted colour spectrum argument to what we know about colour vision. It would be a mind-bending experience, I’m sure! A functionalist might argue that if we were to do this, at some point, inconsistencies between what it is we are being asked to conceive and what is physically possible would emerge.

Of course, there are those who will disagree with my conception of conceivability as outlined above, but let’s address those concerns when we discuss zombies. For now, it is enough to appreciate that it’s easier to imagine alternative scenarios that feel consistent with the laws of physics than it is to articulate a scenario that is consistent with those laws.

---

In my quest to try to answer this week’s question — Is Consciousness Computational? — I first outlined the main argument for this view:

1. Premise 1 (P1): All mental states are functional states. (M → F)

2. Premise 2 (P2): Consciousness is a mental state. (Con → M)

3. Premise 3 (P3): All functional states are computable. (F → C)

4. Conclusion (C): Therefore, consciousness is computable. (Con → C)

So far, we’ve explored one type of argument (the inverted colour spectrum argument) that challenges the idea that consciousness is computational by questioning premises 1 and 2. Let’s move on to a different type of argument against computational functionalism — an argument that challenges premise 3.

2. Quantum Consciousness?

Earlier, I mentioned that computational functionalism subscribes to the idea that mental states do not depend on any specific physical substrate — that is mental states are substrate-independent. Just as computer software can run on different computer hardware, computational functionalism believes that mental states can run on different physical forms as long as the right computational processes are in place.

We know that computations are substrate-independent through the work of Alan Turing and Alonzo Church. During the 1930s, while Alonzo Church was working on lambda calculus, Alan Turing was pondering the limits of computation. Both Church's lambda calculus and Turing's Turing machines, in their separate ways, proved the same thing — anything that can be computed by one system can also be computed by the other. This was a huge deal because it suggested a universal concept of computability.

Whether a computation is run on a silicon-based computer, a quantum computer, or even a hypothetical biological computer, the outcome of the computation remains the same, as long as the logic and rules of the computation are preserved. The physical substrate (silicon chips, quantum bits, biological neurons, etc.) is a medium for computation but does not define the computation itself.

So the question is — is this true for consciousness?

So far, computational models have been highly successful in cognitive science and artificial intelligence. We’ve seen computational models successfully simulate language processing, pattern recognition, and decision-making. For example, large language models (LLMs) like ChatGPT that can generate human-like text and engage in seemingly intelligent conversation, highlight the potential of computational models to mimic aspects of human functioning. The recent success of LLMs has many in the AI and cognitive science community feeling confident that a computational approach to understanding the mind is a viable theory.

But, not everyone is so sure.

It turns out that there are aspects of mathematics that cannot be solved computationally.

Turing's work on computability, alongside Gödel's Incompleteness Theorems, exposes fundamental limitations in formal systems, including those that underpin computational systems based on formal logic. Gödel's theorems reveal that within any sufficiently complex formal system (which could inform a computer's logic), certain propositions will be true but unprovable within the system itself. This suggests an inherent incompleteness in such systems. In other words, there are problems that cannot be solved by any algorithm, even with our most advanced computer systems — these problems are called undecidable problems.

The concept of undecidable problems has sparked some intriguing discussions about consciousness. Some theorists ponder whether consciousness might be one of these elusive, undecidable problems.

This line of reasoning aligns with those of Roger Penrose — a renowned physicist and mathematician — and Stuart Hameroff — an anesthesiologist known for his studies in consciousness. Penrose and Hameroff suggest that consciousness might be explained by quantum phenomena, which are beyond the scope of classical computational models.

In the quantum world, particles like electrons or photons can exist in a superposition, meaning they can be in multiple states simultaneously. This superposition is a delicate condition where the quantum particles are perfectly isolated and not interacting with their environment. It's like they are in their own little world, with their states being a well-kept secret. This state is called quantum coherence.

The moment these quantum particles start interacting with their surroundings (like particles in the air, photons from light, etc.), they start to lose this superposition. This process is called decoherence. It's like the particles can't keep their state a secret anymore because the environment “measures” or interacts with them, causing them to “choose” one state over another.

Penrose and Hameroff suggest that consciousness arises from quantum phenomena within the brain's neural structures, specifically in microtubules, which are components of the cell's structural skeleton. Their theory suggests that quantum superpositions and their subsequent collapse in these microtubules produce moments of conscious awareness orchestrated by classical neural signalling (the theory is called the Orchestrated Objective Reduction theory, or Orch-OR).

If the Orch-OR theory holds, and consciousness is a quantum phenomenon, computational functionalism has a problem.

---

Let’s review the logic of the computational functionalist view one last time:

1. Premise 1 (P1): All mental states are functional states. (M → F)

2. Premise 2 (P2): Consciousness is a mental state. (Con → M)

3. Premise 3 (P3): All functional states are computable. (F → C)

4. Conclusion (C): Therefore, consciousness is computable. (Con → C)

The Orch-OR theory suggests that not all functional states are computable (challenging the notion that F → C), thereby questioning the validity of Premise 3.

---

But the Orch-OR theory encounters a significant challenge.

The Challenge of Decoherence

Max Tegmark — a physicist and cosmologist known for his work in quantum mechanics — argues that for quantum effects to have any meaningful impact on the brain, quantum states would need to maintain their coherence; that is, they would need to preserve a stable phase relationship necessary for quantum computation. However, Tegmark argues that decoherence — the deterioration of this quantum coherence — would occur too quickly in the brain.

Decoherence happens super fast. And it happens especially super fast in warm and wet environments. The human brain is very warm (38.5°C; 101.3F) and very wet (73% water). Any quantum coherence in the brain would deteriorate on the order of .00000000000000000001 (10^-20) to .0000000000001 (10^-13) seconds. Which is very, very, very, fast. Far too quickly to have a meaningful influence on brain processes.

The Orch-OR theory is highly controversial. Many have criticised it for its serious lack of empirical evidence in support of a quantum account of consciousness. Tegmark is one such critic, arguing that classical physics is sufficient to explain the brain and consciousness without needing to resort to quantum explanations.

The Sum Up

So, there you have it! Computational functionalism holds as a possible theory of consciousness — for now. There are, of course, many other arguments and counter-arguments for and against computational functionalism. But I’m going to leave computational functionalism for a bit.

Starting next week, I’m going to begin a short series on the five most controversial ideas in the study of consciousness. Indeed, many would argue that if your theory about consciousness leads you to one of these ideas — you should probably find another theory! But, how bad are these ideas? Can we learn anything from them?

---

In the next issue…

Homunculi in the AI

We often think of consciousness as a movie playing in our heads — like there’s a little person that sits behind our eyes, watching our experiences on a big screen — maybe even directing the show. But when we look inside, of course, we find no miniature version of ourselves — no little screen.

Where does this feeling come from? Why is it so wrong, and what’s really going on?

In the next issue of When Life Gives You AI, I’ll explore the homunculus fallacy — what is it? Whether it’s all that bad? And what it can tell us about conscious AI?

Find it in your inbox on Tuesday, February 6, 2024.